শিরোনাম: গবেষণার নির্ভরযোগ্য হাতিয়ার: Z-Test কী এবং কখন এটি ব্যবহার করবেন?

লেখক: নিউজ ডেস্ক, বিজ্ঞানী অর্গ

গবেষণায় যখন আমরা কোনো সিদ্ধান্তে পৌঁছাতে চাই, তখন একটা প্রশ্ন প্রায়ই সামনে আসে—আমরা যে ফলাফল পেলাম, তা কি নিছক কাকতালীয়, নাকি এর পেছনে বাস্তবিকই কোনো প্রভাব বা পার্থক্য আছে? এই প্রশ্নের উত্তর খুঁজতে সাহায্য করে পরিসংখ্যানের একটি গুরুত্বপূর্ণ হাতিয়ার—Z-Test।

যদিও নামটা শুনে একটু কঠিন মনে হতে পারে, তবে Z-Test আসলে অনেকটা এক্স-রে মেশিনের মতো। ঠিকভাবে ব্যবহার করলে এটি আমাদের বলে দেয়, কোন তথ্য বা নমুনা (sample) আসলে জনসংখ্যার গড় (population mean) থেকে ভিন্ন কিনা, এবং এই ভিন্নতা কি পর্যাপ্ত গুরুত্বপূর্ণ কিনা।

📘 Z-Test কী?

Z-Test একটি পরিসংখ্যানিক পরীক্ষা, যা মূলত হাইপোথিসিস টেস্টিং-এর জন্য ব্যবহৃত হয়। এটি বলে দেয়, একটি নমুনা কোনো নির্দিষ্ট গড় থেকে যথেষ্ট পরিমাণে আলাদা কিনা, অথবা দুটি নমুনার গড়ের মধ্যে প্রকৃত কোনো পার্থক্য আছে কিনা।

এটি মূলত তখনই ব্যবহারযোগ্য, যখন:

• আপনার হাতে একটি বড় নমুনা থাকে (সাধারণত n > 30),
• আপনি জানেন পুরো জনসংখ্যার গড় এবং তার মান বিচ্যুতি (standard deviation),
• এবং আপনার তথ্যগুলি সাধারণ বন্টনের (normal distribution) অনুসারী।

✅ Z-Test ব্যবহারের উপকারিতা

1. নির্ভুল হাইপোথিসিস টেস্টিং:
   Z-Test হাইপোথিসিস টেস্টিং-এর একটি নির্ভরযোগ্য পদ্ধতি। যদি আপনি কোনো নির্দিষ্ট গড় সম্পর্কে ধারণা করেন (যেমন, একটি স্কুলে ছাত্রদের গড় পরীক্ষার নম্বর ৭০), তাহলে Z-Test আপনাকে বলে দেবে, আপনার নমুনা (say, ৩০ জন ছাত্রের ফলাফল) সেই গড়ের সাথে সামঞ্জস্যপূর্ণ কিনা।
2. বিশ্বস্ততা:
   বড় ডেটাসেটের ক্ষেত্রে এবং যেখানে বৈচিত্র্য (variance) জানা থাকে, সেখানে Z-Test খুবই নির্ভরযোগ্য এবং শক্তিশালী প্রমাণ উপস্থাপন করতে পারে।
3. সহজ এবং সুপরিচিত:
   অনেক গবেষক ও ছাত্র Z-Test এর ধারণার সাথে পরিচিত। এটি সহজবোধ্য এবং সরল গাণিতিক ফর্মুলায় কাজ করে, ফলে গবেষণার ফলাফল ব্যাখ্যা করতেও সুবিধা হয়।

❌ ভুল ব্যবহারে বিপদ

যদিও Z-Test খুব কার্যকর, তবে কিছু গুরুত্বপূর্ণ শর্ত না মানলে এর ফলাফল বিপথে নিয়ে যেতে পারে:

1. ছোট নমুনায় প্রয়োগ:
   Z-Test বড় নমুনার জন্য তৈরি। ছোট নমুনায় (n < ৩০) এটি ব্যবহার করলে ফলাফল ভুল হতে পারে। এ ক্ষেত্রে T-Test বেশি উপযুক্ত।
2. স্বাভাবিক বন্টন না থাকা:
   Z-Test ধরে নেয় যে আপনার ডেটা স্বাভাবিকভাবে বিতরণ করা। যদি তা না হয়, তাহলে ফলাফল বিভ্রান্তিকর হতে পারে।
3. অজানা ভ্যারিয়েন্সে প্রয়োগ:
   Z-Test সঠিকভাবে কাজ করে তখনই, যখন আপনি জনসংখ্যার মান বিচ্যুতি (standard deviation) জানেন। না জানলে, ফলাফল অচল বা ভুল হতে পারে।
4. অন্ধভাবে নির্ভর করা:
   শুধুমাত্র Z-Test এর উপর নির্ভর করে গবেষণা করলে গবেষণার মান কমে যেতে পারে। আপনাকে বুঝে নিতে হবে, এটি কোথায় কার্যকর আর কোথায় নয়।

🔁 আধুনিক বিকল্প

বর্তমানে আরও কিছু আধুনিক পদ্ধতি রয়েছে যা Z-Test এর সীমাবদ্ধতা কাটিয়ে উঠতে পারে, যেমন:

• Bayesian Methods: অনুমান নির্ভর নয়, বরং প্রাথমিক বিশ্বাস (prior belief) ও ডেটার ভিত্তিতে সিদ্ধান্ত দেয়।
• Bootstrapping: পুনরায় নমুনা গ্রহণ করে যে-কোনো ধরণের ডেটা নিয়েও বিশ্লেষণ করতে পারে, এমনকি ছোট ডেটাসেটেও।

🛠️ বাস্তবে Z-Test কীভাবে করবেন?

প্রোগ্রামিং ল্যাঙ্গুয়েজ ব্যবহার করে Z-Test করা খুব সহজ।

🔹 R ভাষায়:
BSDA প্যাকেজের z.test() ফাংশন ব্যবহার করে Z-Test করতে পারেন। উদাহরণ:

library(BSDA)
z.test(x = sample_data, mu = 70, sigma.x = 10)

🔹 Python ভাষায়:
statsmodels লাইব্রেরির ztest() ফাংশন ব্যবহার করুন। উদাহরণ:

from statsmodels.stats.weightstats import ztest
ztest(data, value=70)

📊 ফলাফল বিশ্লেষণ

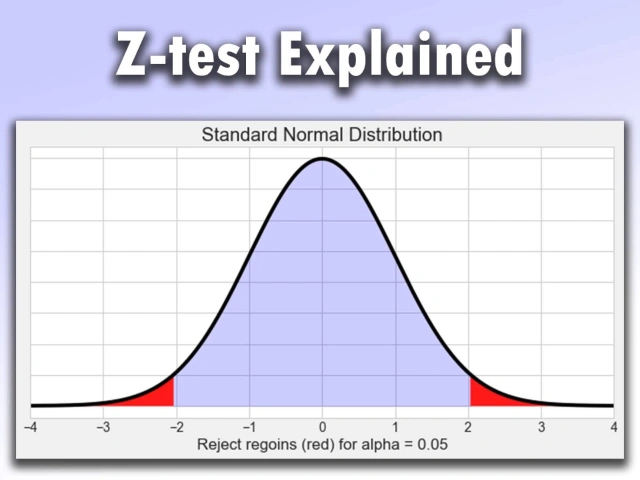
Z-Test এর ফলাফল থেকে আপনি একটি Z মান (Z-value) এবং একটি p-value পাবেন।

• Z মান মূলত ডেটার অবস্থান নির্ধারণ করে একটি স্বাভাবিক বিতরণের স্কেলে।
• p-value আপনাকে বলে দেয়, এই ফলাফলটি কাকতালীয়ভাবে আসা সম্ভবনা কতটা।

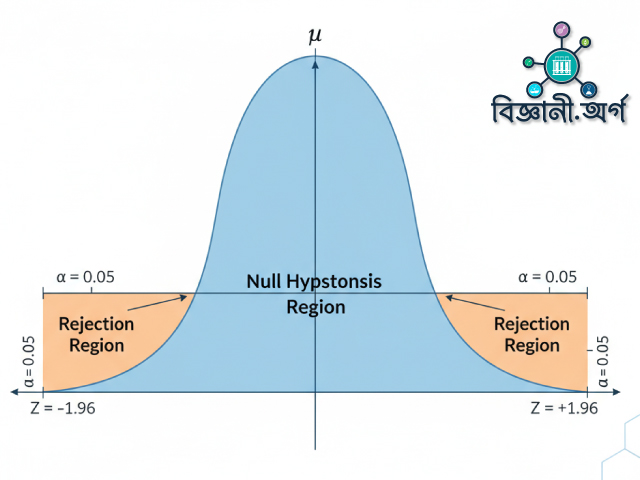
ধরা যাক, আপনি ৫% (α = 0.05) সিগনিফিকেন্স লেভেল ব্যবহার করছেন। তাহলে Z মান যদি ±1.96 এর বাইরে যায়, তাহলে আপনি null hypothesis (যে ধারণা আপনি যাচাই করছেন) প্রত্যাখ্যান করতে পারেন। নিচের এই উইকিপিডিয়ার চিত্রটি এই ধারণাটি ব্যাখ্যা করে:

🔗 Null Hypothesis Region Visual

🎓 আরও শিখতে চান?

আপনি যদি Z-Test এবং আরও অনেক গুরুত্বপূর্ণ পরিসংখ্যানিক পদ্ধতি বিশদভাবে শিখতে চান, তাহলে নিচের অনলাইন কোর্সটি দেখতে পারেন:

📚 Statistical Methods in R
➡️ কোর্স লিংক: https://statisticsglobe.com/online-course-statistical-methods-r

এই কোর্সে আপনি শিখবেন কীভাবে গবেষণায় Z-Test এবং অন্যান্য টুলস সঠিকভাবে ব্যবহার করবেন, এবং কীভাবে এগুলো দিয়ে আপনি আরও নির্ভরযোগ্য সিদ্ধান্তে পৌঁছাতে পারেন।

🔍 উপসংহার

Z-Test একটি সহজ, কার্যকর, এবং বহু ব্যবহৃত পরিসংখ্যানিক পদ্ধতি। তবে এর নির্ভুলতা নির্ভর করে এর শর্তগুলো ঠিকভাবে পূরণ হচ্ছে কিনা তার উপর। গবেষণার মান নিশ্চিত করতে হলে, শুধু Z-Test নয়, বরং অন্য আধুনিক পদ্ধতিগুলোকেও বিবেচনায় নেওয়া উচিত।

বিশ্ববিদ্যালয়ের শিক্ষার্থী থেকে শুরু করে পেশাদার গবেষক পর্যন্ত—Z-Test শেখা ও বোঝা প্রত্যেকের জন্যই গুরুত্বপূর্ণ। কারণ এটি শুধু পরীক্ষার ফলাফল নয়, বরং বাস্তব জীবনের অনেক সিদ্ধান্তেও আলো ফেলতে পারে।